В геометрии треугольника существует важное свойство, касающееся суммы его углов. Это фундаментальное положение помогает решать множество геометрических задач.
Содержание
Основная теорема о сумме углов треугольника
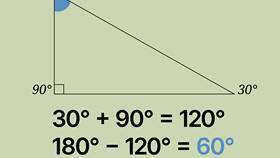
Сумма внутренних углов любого треугольника всегда равна 180 градусам. Это свойство не зависит от вида треугольника (остроугольный, прямоугольный, тупоугольный) и его размеров.
| Тип треугольника | Сумма углов |
| Остроугольный | 180° |
| Прямоугольный | 180° |
| Тупоугольный | 180° |
Что такое смежные углы треугольника
Смежные углы треугольника - это углы, прилегающие к одной стороне. Важно понимать, что:
- Каждый внутренний угол треугольника имеет два смежных угла
- Сумма смежных углов при вершине равна 180° минус величина угла при этой вершине
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним
Пример расчета смежных углов
Рассмотрим треугольник ABC с углами: ∠A = 60°, ∠B = 70°, ∠C = 50°.
- Сумма внутренних углов: 60° + 70° + 50° = 180°
- Смежные углы для стороны AB: ∠A + ∠B = 60° + 70° = 130°
- Внешний угол при вершине C: 180° - 50° = 130° (или ∠A + ∠B = 60° + 70° = 130°)
Практическое применение свойства
| Применение | Описание |
| Решение задач | Позволяет находить неизвестные углы |
| Доказательство теорем | Используется в доказательствах многих геометрических положений |
| Построение фигур | Помогает правильно конструировать треугольники |
Важные следствия
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним
- Сумма всех внешних углов треугольника равна 360°
- В прямоугольном треугольнике два острых угла в сумме дают 90°
Заключение
Знание о том, что сумма углов треугольника равна 180 градусам, является базовым в геометрии. Это свойство позволяет решать широкий круг задач, от простых вычислений до сложных доказательств. Понимание свойств смежных углов расширяет возможности работы с треугольниками и другими геометрическими фигурами.